شبکه‌های کانولوشنی گراف (Graph Convolutional Networks)

در این مطلب، دربارهٔ شبکه‌های کانولوشنی گراف (GCNs) صحبت خواهیم کرد که هدفشان تعمیم عملیات کانولوشن به دامنهٔ گراف است. از آن‌جایی که شبکه‌های عصبی کانولوشنی (CNNs) در حوزهٔ یادگیری عمیق موفقیت چشمگیری داشته‌اند، تعریف عملیات کانولوشن برای گراف‌ها نیز کاملاً طبیعی و منطقی به‌نظر می‌رسد. پیشرفت‌ها در این زمینه معمولاً به دو دستهٔ کلی تقسیم می‌شوند: رویکردهای طیفی (spectral) و رویکردهای مکانی (spatial). از آن‌جایی که در هر کدام از این دو دسته مدل‌های متنوع زیادی وجود دارد، در این مطلب فقط به معرفی چند مدل کلاسیک و مهم بسنده می‌کنیم.

روش‌های طیفی

رویکردهای طیفی (Spectral Approaches) با استفاده از نمایش طیفی (Spectral Representation) گراف‌ها کار می‌کنند. در این بخش، دربارهٔ چهار مدل کلاسیک صحبت خواهیم کرد: شبکه طیفی (Spectral Network)، چب‌نت (ChebNet)، GCN، و AGCN.

شبکه طیفی

🧠 ایدهٔ اصلی شبکه‌های طیفی چیست؟ 

در شبکه‌های عصبی کانولوشنی (CNN)، ما فیلترهایی داریم که روی تصاویر حرکت می‌کنند و الگوهایی مثل لبه‌ها، گوشه‌ها و بافت‌ها را یاد می‌گیرند. حالا سؤال این است که اگر داده‌هایمان به جای تصویر، یک گراف مثل شبکه اجتماعی باشد، چطور می‌توانیم روی آن کانولوشن انجام دهیم؟

🌐 از فضای گراف به فضای فرکانس

در شبکه طیفی، به‌جای اینکه مثل CNN فیلتر را مستقیماً روی گراف حرکت بدهیم، می‌گوییم:

گراف را تجزیه طیفی (Spectral Decomposition) کنیم، یعنی چیزی شبیه تبدیل فوریه روی گراف انجام بدهیم.

فرض کنید که ویژگی‌های گره‌ها مثل دمای هوا در شهرهای مختلف باشند. بعضی مناطق نوسانات شدید دارند (گرم و سرد)، بعضی یکنواخت‌اند. ما می‌توانیم این داده‌ها را به زبان "فرکانس" ترجمه کنیم. همان‌طور که یک آهنگ را می‌شود با ترکیب نُت‌ها (فرکانس‌ها) بازسازی کرد، اطلاعات روی گراف هم می‌توانند با ترکیب ویژه‌بردارهای لاپلاسین (که ستون‌هایش پایه‌هایی از فضای گراف هستند) بازسازی شوند.

عملیات کانولوشن (convolution) در این مدل در حوزهٔ فوریه (Fourier domain) تعریف می‌شود؛ به‌طوری که با انجام تجزیهٔ ویژه (eigendecomposition) روی لاپلاسین گراف، کانولوشن انجام می‌شود. این عملیات را می‌توان به‌صورت ضرب یک سیگنال \(x \in \mathbb{R}^N\) (که به هر گره یک مقدار اسکالر نسبت می‌دهد) در یک فیلتر طیفی \(g_{\theta}\)​ تعریف کرد. این فیلتر به‌صورت ماتریس قطری تعریف می‌شود:\[\mathbf{g}_\theta = \text{diag}(\theta), \quad \theta \in \mathbb{R}^N\]

سپس، کانولوشن گرافی به‌صورت زیر تعریف می‌شود: \[\mathbf{g}_\theta \ast \mathbf{x} = \mathbf{U} \mathbf{g}_\theta(\Lambda) \mathbf{U}^T \mathbf{x}\]

که در آن:

• \(U\) ماتریس بردارهای ویژه (eigenvectors) لاپلاسین نرمال‌شدهٔ گراف است.

• لاپلاسین نرمال‌شده گراف به صورت زیر تعریف می‌شود: \[\mathbf{L} = \mathbf{I}_N - \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} = \mathbf{U} \Lambda \mathbf{U}^T\]

که در فرمول بالا داریم:

• $\backslash (D\backslash )$: ماتریس درجهٔ گره‌ها (degree matrix)

• $\backslash (A\backslash )$: ماتریس مجاورت گراف (adjacency matrix)

• $\backslash (\backslash Lambda\backslash )$: ماتریس قطری مقادیر ویژهٔ لاپلاسین

یکی از مشکلات مدل Bruna (Spectral Network) این بود که:

• فیلترها فقط در فضای فرکانس تعریف می‌شدند؛ بنابراین

• مشخص نبود کجا از گراف (کدام گره یا ناحیه) را بیشتر تحت تأثیر قرار می‌دهند.

• در واقع فیلترها غیرموضعی (non-localized) بودند.

Henaff و همکاران آمدند و با استفاده از ضرایب نرم (smooth coefficients) تلاش کردند کاری کنند که فیلترها اثر موضعی داشته باشند — یعنی مثلاً فقط همسایه‌های نزدیک یک گره را تحت تأثیر قرار بدهند (چیزی مثل فیلتر ۳×۳ در CNN روی تصویر).

CHEBNET

Hammond پیشنهاد می‌دهد که فیلتر طیفی \(g_{\theta}(\Lambda)\) را می‌توان با یک بسط چندجمله‌ای چبیشف \(T_k(x)\) تا مرتبهٔ \(K\) تقریب زد. بنابراین، عملیات کانولوشن به‌صورت زیر بازنویسی می‌شود:

\begin{equation} g_\theta \star \mathbf{x} \approx \sum_{k=0}^{K} \theta_k \, T_k(\tilde{\mathbf{L}}) \, \mathbf{x} \end{equation}

که در آن، \(\tilde{\mathbf{L}}\) نسخهٔ مقیاس‌دار لاپلاسین نرمال‌سازی‌شده است و به صورت زیر تعریف می‌شود: 

\begin{equation} \tilde{\mathbf{L}} = \frac{2}{\lambda_{\text{max}}} \mathbf{L} - \mathbf{I}_N \end{equation}

در این فرمول، \(\lambda_{\text{max}}\) بزرگ‌ترین مقدار ویژه از ماتریس لاپلاسین \(\mathbf{L}\) است و \( \theta \in \mathbb{R}^K\) برداری از پارامترهای قابل یادگیری است.

برای پیاده‌سازی فیلتر چبیشف، از تعریف بازگشتی چندجمله‌ای‌های چبیشف استفاده می‌شود:

\begin{align} T_0(\mathbf{x}) &= 1 \\ T_1(\mathbf{x}) &= \mathbf{x} \\ T_k(\mathbf{x}) &= 2 \mathbf{x} \cdot T_{k-1}(\mathbf{x}) - T_{k-2}(\mathbf{x}) \quad \text{for } k \geq 2 \end{align}

📌 نکته کلیدی:

این کانولوشن به‌صورت $\backslash (K\backslash )$-localized است، چرا که از \(K\)-امین چندجمله‌ای لاپلاسین استفاده می‌کند، و در نتیجه تنها گره‌هایی تا شعاع $\backslash (K\backslash )$ همسایگی در محاسبات شرکت دارند.

مزیت مهم این مدل نسبت به شبکه طیفی این است که:

دیگر نیازی به محاسبهٔ مقادیر ویژه و بردارهای ویژه (eigendecomposition) ماتریس لاپلاسین نیست. که این موضوع باعث می‌شود ChebNet هم سریع‌تر باشد و هم برای گراف‌های بزرگ‌تر بهتر مقیاس‌پذیر باشد.

یک مثال برای فیلترینگ Chebnet در یک گراف خطی با 5 گره:

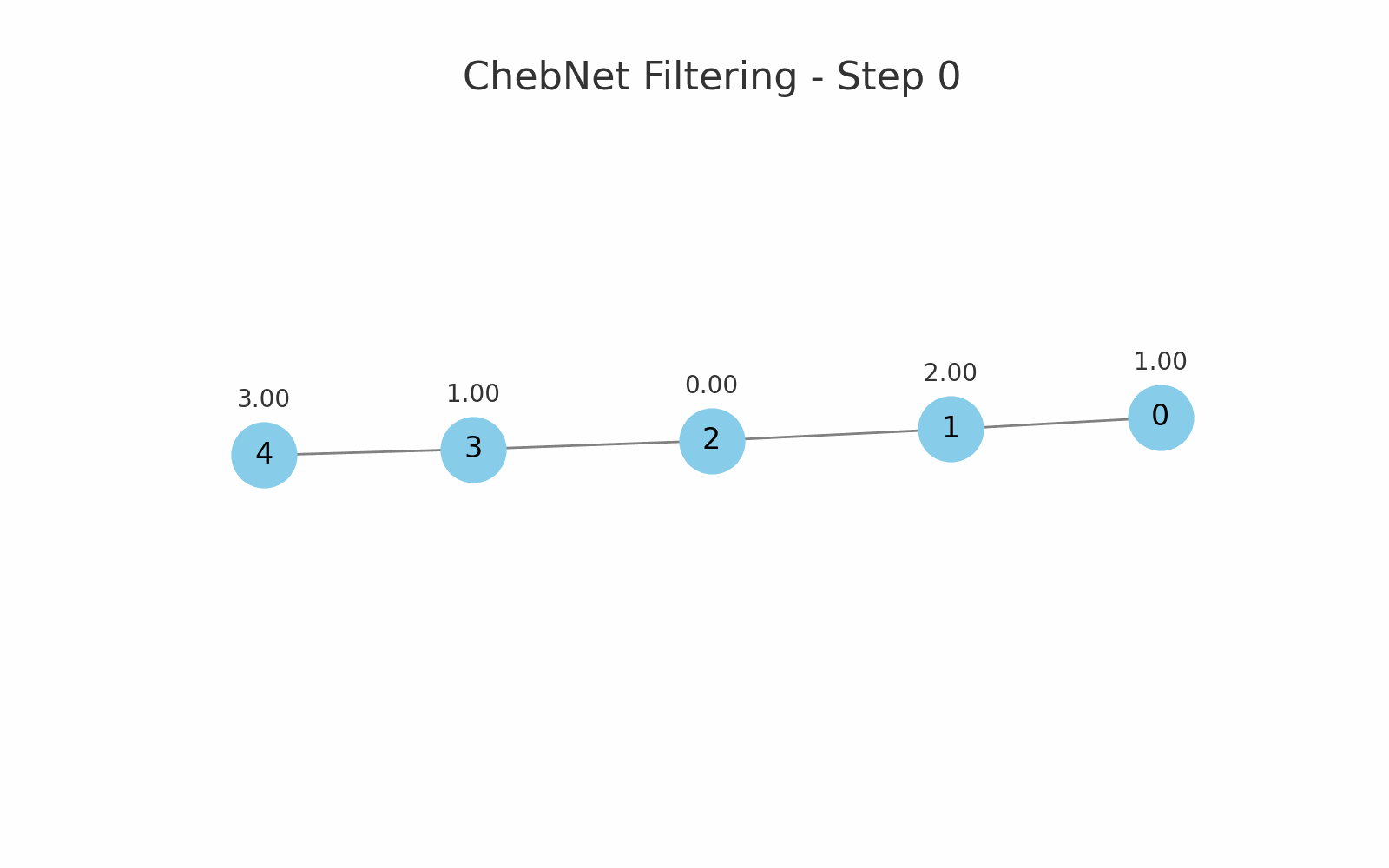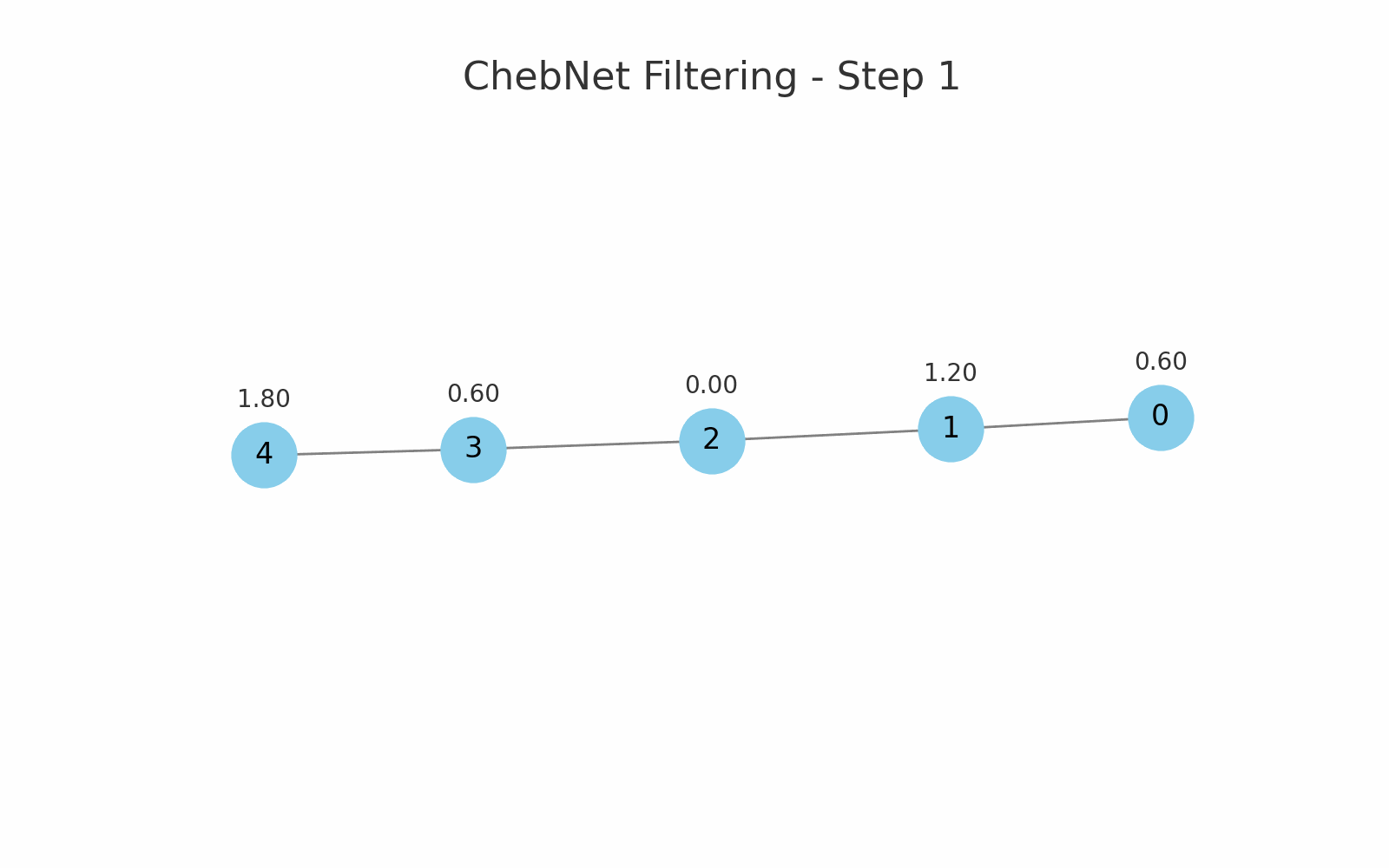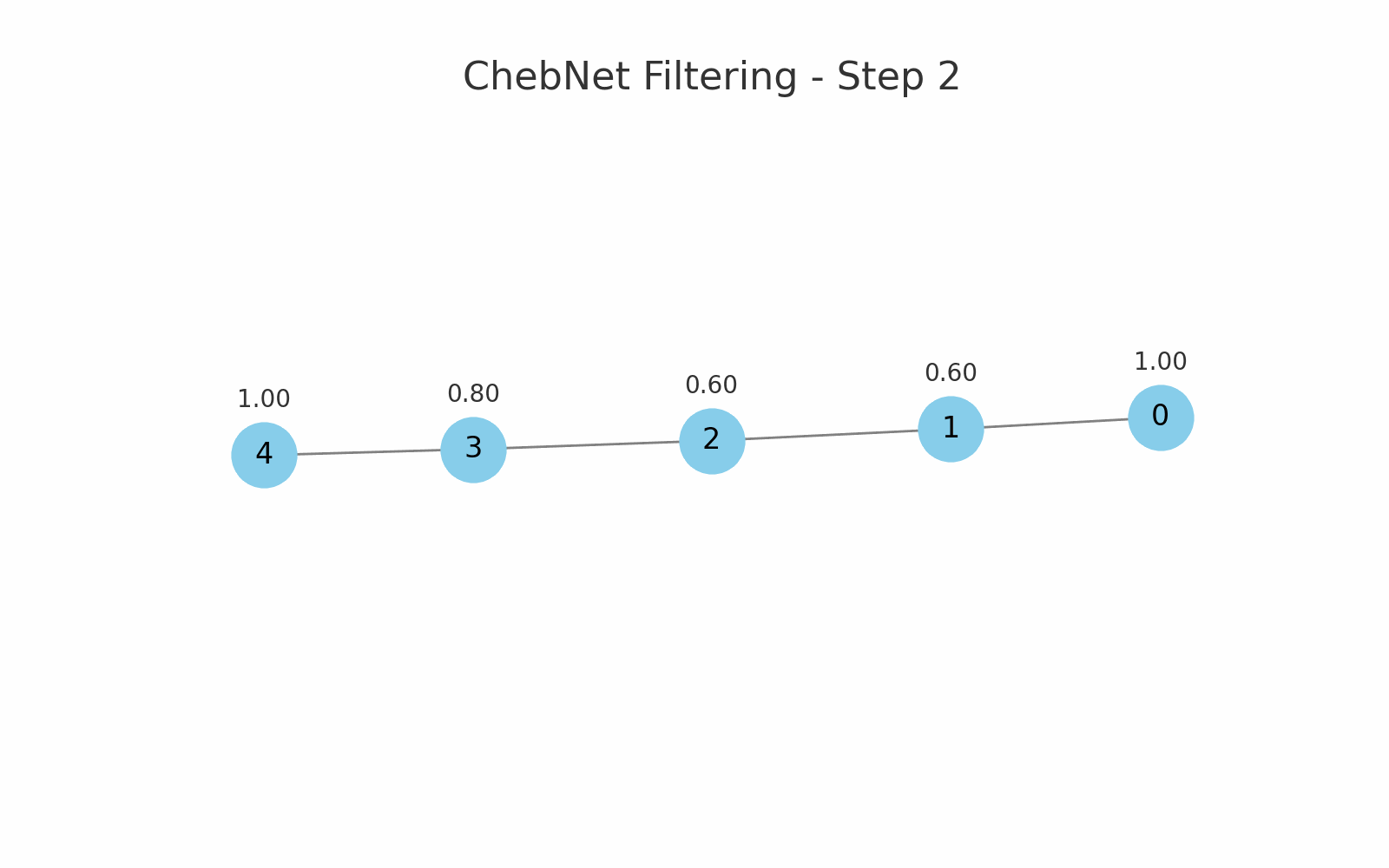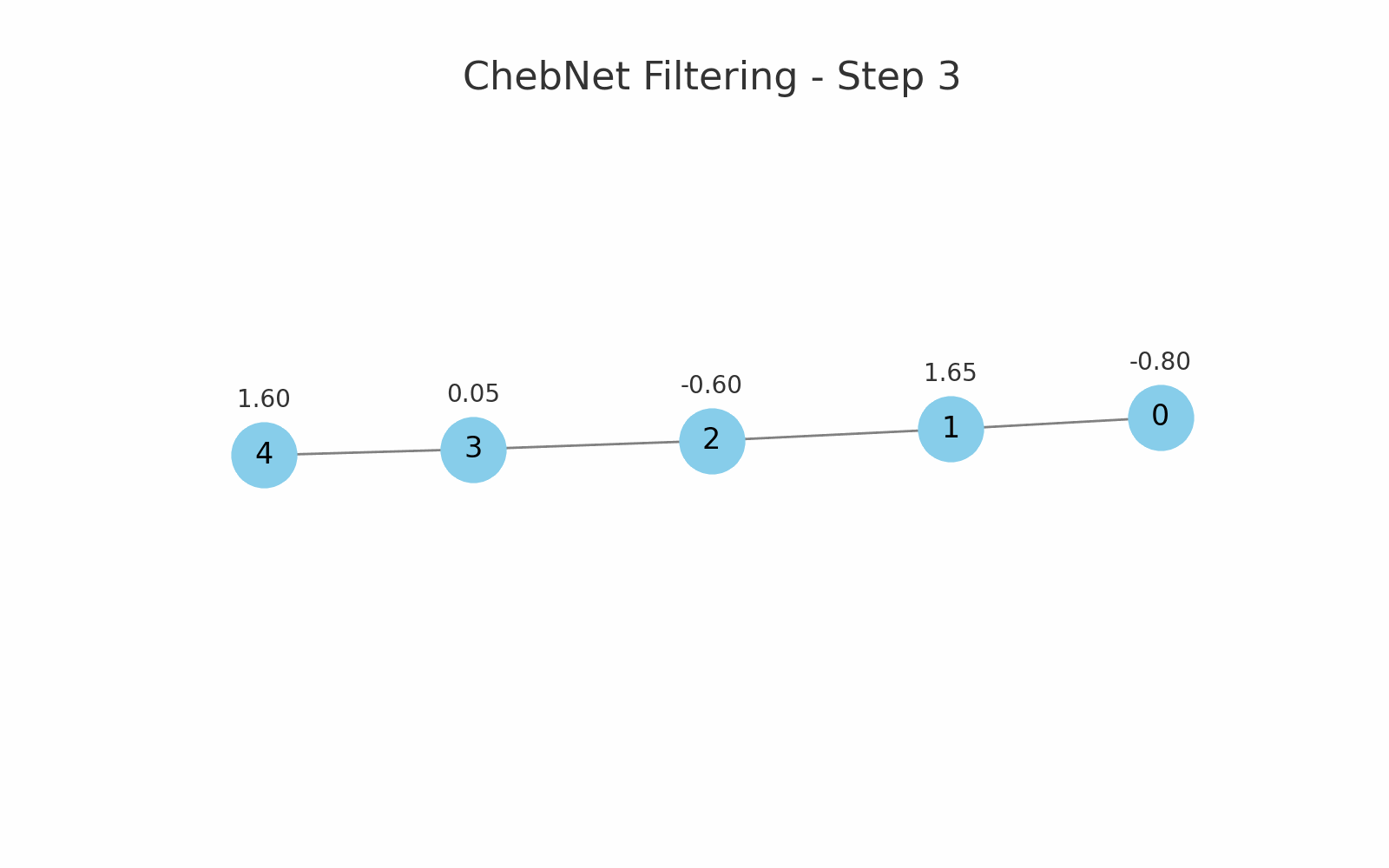
حال برای یک گراف، کد پایتونی محاسبۀ Chebnet را می‌نویسیم:

import numpy as np
import networkx as nx

G = nx.path_graph(5)

x = np.array([1, 2, 0, 1, 3], dtype=float)  # shape: (5,)

A = nx.to_numpy_array(G)               
D = np.diag(np.sum(A, axis=1))
L = D - A 

L_norm = np.linalg.inv(D) @ L             # L_norm = D^{-1} * L

def chebyshev_polynomials(L, K):
    T = [np.identity(L.shape[0]), L]  # T0 = I , T1 = L
    for k in range(2, K+1):
        T_k = 2 * L @ T[-1] - T[-2]   # T_k = 2L T_{k-1} - T_{k-2}
        T.append(T_k)
    return T

T_list = chebyshev_polynomials(L_norm, K=2)

theta = [0.6, -0.4, 0.3]

x_out = sum(theta[i] * (T_list[i] @ x) for i in range(len(theta)))

print(x)
print(x_out)

برای ورودی‌های زیر (ویژگی گره‌ها):

[1.0, 2.0, 0.0, 1.0, 3.0]

خروجی‌های زیر را (برای ویژگی گره‌ها) خواهیم داشت:

[−0.8, 1.65, −0.6, 0.05, 1.6]

GCN

Kipf و Welling برای ساده‌سازی مدل‌های طیفی قبلی، پیشنهاد کردند که ترتیب فیلتر (در ChebNet یا SpectralNet) را به $\backslash (K=1\backslash )$ محدود کنیم. این کار باعث کاهش بیش‌برازش (overfitting) در گراف‌هایی می‌شود که توزیع درجه گره در آن‌ها بسیار متنوع است.

برای ساده‌سازی بیشتر، مقدار بیشینه مقدار ویژه (eigenvalue) لاپلاسی \(\lambda_{max}=2\) فرض می‌شود.  با این فرض‌ها، معادله‌ی طیفی به شکل ساده‌تری نوشته می‌شود:

\[ g_{\theta'} \star \mathbf{x} \approx \theta'_0 \mathbf{x} + \theta'_1 (\mathbf{L} - \mathbf{I}_N) \mathbf{x} = \theta'_0 \mathbf{x} - \theta'_1 \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} \mathbf{x}  \]

با قراردادن شرط \(\theta = \theta'_0 = \theta'_1\)، این معادله به‌صورت زیر در می‌آید:

\[ g_{\theta} \star \mathbf{x} \approx \theta \left( \mathbf{I}_N + \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} \right) \mathbf{x}  \]

⚠️ مشکل عددی و راه‌حل

انباشتن چندین لایه از این عملیات ممکن است به مشکلات عددی مثل vanishing/exploding gradients بینجامد. برای حل این مشکل، Kipf و Welling ترفند بازنرمال‌سازی (renormalization trick) را پیشنهاد دادند:

\[ \mathbf{I}_N + \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} \quad \longrightarrow \quad \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \]

که در آن:

• \( \tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I}_N \): افزودن ارتباط خودگره (self-loop)

• \( \tilde{D}_{ii} = \sum_j \tilde{A}_{ij} \): درجهٔ گره‌های جدید با self-loop

تعمیم برای داده‌های چندبعدی

اگر هر گره چند ویژگی داشته باشد (مثلاً $\backslash (C\backslash )$ کانال ورودی و \(F\) کانال خروجی)، آنگاه کانولوشن به‌صورت زیر تعمیم می‌یابد:

\[ \mathbf{Z} = \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \boldsymbol{\Theta}  \]

که در آن:

• \(\mathbf{X} \in \mathbb{R}^{N \times C}\):  ماتریس ویژگی ورودی گره‌ها
• \(\boldsymbol{\Theta} \in \mathbb{R}^{C \times F}\): وزن‌های قابل آموزش (فیلترها)
• \(\mathbf{Z} \in \mathbb{R}^{N \times F}\): ویژگی خروجی برای هر گره

📌 با توجه به روندی که برای GCN داشتیم می‌توانیم بگوییم که GCN از رویکرد طیفی (Spectral) شروع شده است، ولی طوری ساده‌سازی شده که در نهایت رفتارش شبیه Spatial هست.

AGCN

مدل‌های قبلی مثل GCN و ChebNet فقط از ساختار گراف اولیه (یعنی ماتریس مجاورت داده‌شده) استفاده می‌کردند. اما AGCN به این نکته توجه می‌کند که ممکن است روابط پنهان یا ضمنی بین گره‌ها وجود داشته باشد که در ساختار اولیه نیامده‌اند. بنابراین AGCN (Adaptive Graph Convolution Network) یک لاپلاسی باقیمانده (residual graph Laplacian) یاد می‌گیرد و آن را به لاپلاسی اولیه اضافه می‌کند:\[\hat{\mathbf{L}} = \mathbf{L} + \alpha \mathbf{L}_{\text{res}}\]

که در آن $\backslash (\backslash alpha\backslash )$ یک پارامتر قابل یادگیری یا تنظیم‌پذیر است.

تعریف لاپلاسی باقیمانده (Residual Laplacian):\[\mathbf{L}_{\text{res}} = \mathbf{I} - \hat{\mathbf{D}}^{-\frac{1}{2}} \hat{\mathbf{A}} \hat{\mathbf{D}}^{-\frac{1}{2}}\]

و:\[\hat{\mathbf{D}} = \text{degree}(\hat{\mathbf{A}})\]

که \(\hat{\mathbf{A}}\) ماتریس مجاورت یادگرفته‌شده است.

چطور \(\hat{\mathbf{A}}\) یاد گرفته می‌شود؟

برای یادگیری \(\hat{\mathbf{A}}\)، مدل از یک فاصلهٔ ماهالانوبیس تعمیم‌یافته بین ویژگی‌های گره‌ها استفاده می‌کند:\[D(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{(\mathbf{x}_i - \mathbf{x}_j)^T \mathbf{M} (\mathbf{x}_i - \mathbf{x}_j)}\]

که در آن \(\mathbf{M} = \mathbf{W}_d \mathbf{W}_d^\top \) ​یک پارامتر قابل یادگیری است. 

سپس فاصلهٔ بین گره‌ها به شباهت (similarity) تبدیل می‌شود:

\[G_{x_i, x_j} = \exp \left( - \frac{D(\mathbf{x}_i, \mathbf{x}_j)}{2\sigma^2} \right)\]

و در نهایت با نرمال‌سازی این شباهت‌ها، ماتریس مجاورت جدید \(\hat{\mathbf{A}}\) ساخته می‌شود. 

روش‌های مکانی (Spatial Methods)

🔸 در روش‌های طیفی که قبلاً بررسی کردیم (مثل Spectral Network، ChebNet، GCN و AGCN)، فیلترهایی که مدل یاد می‌گیرد به پایه‌ی ویژه (eigenbasis) لاپلاسین گراف وابسته هستند.

❗ این یعنی اگر مدل روی یک گراف خاص آموزش دیده باشد، نمی‌توان آن را مستقیماً روی یک گراف دیگر با ساختار متفاوت به کار برد، چون پایه‌های ویژه تغییر می‌کنند!

 🧠 راه‌حل: روش‌های مکانی (Spatial)

🔹 بر خلاف روش‌های طیفی، روش‌های مکانی مستقیماً روی خود گراف عمل می‌کنند. یعنی:

• کانولوشن روی گره‌ها انجام می‌شود،

• فقط همسایه‌های نزدیک فضایی را در نظر می‌گیرند.

بنابراین، فیلترها به جای اینکه روی فضای طیفی تعریف شوند، مثل CNNهای سنتی روی همسایگی‌های محلی تعریف می‌شوند.

❗ چالش اصلی روش‌های مکانی

تعریف عملیات کانولوشن با وجود همسایگی‌های با اندازه‌های متفاوت در گراف‌ها، و در عین حال حفظ ناحیه‌گرایی (locality) که در CNNها وجود دارد.

یعنی باید طوری طراحی شوند که:

• در هر گره با تعداد همسایه متفاوت، عمل کانولوشن قابل تعریف باشد،

• اما در عین حال، خواص "محلی بودن" حفظ شود، مثل CNNها روی تصویر.

NEURAL FPS

Duvenaud از ماتریس‌های وزن متفاوت برای گره‌هایی با درجات مختلف استفاده می‌کنند. ابتدا مدل، embedding مربوط به گره \(v\) را در لایهٔ قبلی به همراه embedding گره‌های همسایه‌اش جمع می‌زند:\[\mathbf{x} = \mathbf{h}_v^{t-1} + \sum_{i=1}^{|N_v|} \mathbf{h}_i^{t-1}\]

سپس آن را از طریق یک تابع فعال‌سازی (مثل ReLU یا sigmoid) و ضرب در ماتریس وزن متناسب با درجهٔ گره تبدیل می‌کند:

\[\mathbf{h}_v^{t} = \sigma\left(\mathbf{x} \mathbf{W}_t^{|N_v|}\right)\]

در اینجا:

• \(\mathbf{W}_t^{|N_v|}\): ماتریس وزن برای گره‌هایی با درجهٔ ​\(|N_v|\) در لایهٔ \(t\) است.

• \(\mathbf{h}_v^{t}\): embedding گره \(v\) در لایۀ \(t\)

• $\backslash (N\_v\backslash )$: مجموعهٔ همسایه‌های گره $\backslash (v\backslash )$

این مدل سعی دارد برای هر گره، با توجه به تعداد همسایه‌هایش (یعنی درجه‌اش)، یادگیری متمایزی انجام دهد. گره‌هایی با درجات مختلف می‌توانند ساختار و نقش متفاوتی در گراف داشته باشند، پس منطقی است که از پارامترهای متفاوتی برای یادگیری آن‌ها استفاده شود.

برای گراف‌های بزرگ که گره‌ها درجه‌های متنوعی دارند (مثلاً گره‌ای با 3 همسایه، یکی با 10، یکی با 100 و ...) باید تعداد زیادی ماتریس وزن یاد گرفته شود که یادگیری و مقیاس‌پذیری مدل را با چالش مواجه می‌کند.

مثال:

در مثال بالا، یک گراف ساده شامل دو بخش داریم:

• گره 0 با سه همسایه: $1,2,3$

• گره 4 با یک همسایه: 5

ویژگی‌های اولیه (Initial Features)

ویژگی‌های اولیه هر گره در داخل گره نوشته شده‌اند (مثلاً گره 0 مقدار ویژگی‌اش 1.0 است).

فرایند به‌روزرسانی ویژگی در Neural FPS

طبق فرمول:

\[\mathbf{x} = \mathbf{h}_v^{t-1} + \sum_{i \in \mathcal{N}(v)} \mathbf{h}_i^{t-1}\]

\[\mathbf{h}_v^t = \sigma \left( \mathbf{x} \cdot \mathbf{W}_t^{|\mathcal{N}_v|} \right)\]

برای مثال:

• گره 0:

\[ x = 1.0 + 0.5 + 0.5 + 0.5 = 2.5 \quad \text{and since } W_3 = 0.5 \Rightarrow h_0^t = 2.5 \times 0.5 = 1.25 \]

• گره 4:

\[ x = 2.0 + 1.0 = 3.0 \quad \text{and since } W_1 = 2.0 \Rightarrow h_4^t = 3.0 \times 2.0 = 6.0 \]

یک مثال با کتابخانۀ PyG پیاده‌سازی کرده‌ایم که به صورت زیر است:

import torch
import torch.nn.functional as F
from torch.nn import Linear, ModuleDict
from torch_geometric.nn import MessagePassing
from torch_geometric.data import Data

class NeuralFPSLayer(MessagePassing):
    def __init__(self, in_channels, out_channels, max_degree=10):
        super().__init__(aggr='add')  # or 'mean'
        self.degrees = max_degree + 1
        self.linears = ModuleDict({
            str(d): Linear(in_channels, out_channels)
            for d in range(self.degrees)
        })

    def forward(self, x, edge_index):
        row, col = edge_index
        deg = torch.bincount(row, minlength=x.size(0))

        out = self.propagate(edge_index, x=x)

        out = out + x

        # Apply degree-specific transformation
        transformed = torch.zeros_like(out)
        for d in range(self.degrees):
            idx = (deg == d).nonzero(as_tuple=True)[0]
            if len(idx) > 0:
                transformed[idx] = self.linears[str(d)](out[idx])
        return F.relu(transformed)

edge_index = torch.tensor([[0, 0, 0, 1, 2, 3, 4],
                           [1, 2, 3, 0, 0, 0, 5]], dtype=torch.long)
x = torch.tensor([[1.0], [0.5], [0.5], [0.5], [2.0], [1.0]]) 

data = Data(x=x, edge_index=edge_index)

layer = NeuralFPSLayer(in_channels=1, out_channels=1, max_degree=3)
output = layer(data.x, data.edge_index)

print("Updated features:\n", output)

خروجی این کد به صورت زیر می‌تواند باشد:

Updated features:
 tensor([[0.0000],
        [0.4153],
        [0.4153],
        [0.4153],
        [0.5759],
        [0.0000]], grad_fn=<ReluBackward0>)

PATCHY-SAN

مدل PATCHY-SAN روشی است برای اعمال عملیات کانولوشن روی گراف‌ها، مشابه با کاری که CNNها در تصاویر انجام می‌دهند. برخلاف مدل‌های دیگر، این روش برای تعریف ساختارهای موضعی (receptive fields) از یک رویکرد نظم‌بخش استفاده می‌کند.

✴️ مراحل اصلی PATCHY-SAN:

1. Node Sequence Selection (انتخاب توالی گره‌ها):

به‌جای پردازش کل گراف، PATCHY-SAN ابتدا فقط برخی از گره‌ها را انتخاب می‌کند.
برای این کار:

• از روش‌های برچسب‌گذاری گراف برای تعیین ترتیب گره‌ها استفاده می‌کند (مثل رتبه‌بندی درجه یا مرکزی بودن).

• سپس با یک گام پرشی $\backslash (s\backslash )$، از این توالی، $\backslash (w\backslash )$ گره را انتخاب می‌کند.

2. Neighborhood Assembly (ساخت همسایگی):

برای هر گره انتخاب‌شده، ناحیه همسایگی آن ساخته می‌شود:

• ابتدا همسایگان 1-پرش (1-hop) را انتخاب می‌کند.

• اگر کافی نبود، همسایگان سطح بالاتر را اضافه می‌کند تا به تعداد \(k\) گره برسد.

3. Graph Normalization (نرمال‌سازی گراف):

هدف این مرحله مرتب‌سازی گره‌های همسایه است:

• چون ساختار گراف ترتیب ندارد، باید گره‌ها را در فضای برداری به شکلی ثابت و قابل‌مقایسه نمایش داد.

• ایده: اگر دو گره در گراف‌های مختلف نقش ساختاری مشابه دارند، در بردار نهایی جایگاه مشابهی بگیرند.

• این بخش هستهٔ PATCHY-SAN است.

4. Convolutional Architecture (معماری کانولوشن):

• حالا می‌توان با استفاده از معماری‌های CNN، ویژگی‌های نواحی نرمال‌شده را پردازش کرد.

• ویژگی گره‌ها و یال‌ها مانند کانال‌های ورودی به CNN در نظر گرفته می‌شوند.

PATCHY-SAN تلاش می‌کند گراف را مثل تصویر کند؛ یعنی به جای اینکه گراف به‌صورت ساختار نامنظم باقی بماند، آن را به یک شبکهٔ موضعی، با ترتیب مشخص از گره‌ها، تبدیل می‌کند و سپس کانولوشن را اجرا می‌کند.