مقدمه‌ای بر شبکه‌های انتشار (Diffusion Models)

آیا تا به حال فکر کرده‌اید که چگونه هوش مصنوعی می‌تواند تصاویر شگفت‌انگیزی خلق کند؟ یکی از قدرتمندترین تکنیک‌های این حوزه، مدل‌های انتشار (Diffusion Models) هستند. تصور کنید یک عکس با جزئیات دارید. حالا به تدریج نویز به آن اضافه می‌کنیم، نویز به صورت تصادفی به تصویر اضافه می‌شود و تصویر به مرور زمان محو و غیرقابل تشخیص می‌شود. در نهایت، تصویر به یک حجم کامل از نویز تبدیل می‌شود.

مدل‌های انتشار دقیقاً این کار را انجام می‌دهند، اما به صورت معکوس! آنها با شروع از نویز تصادفی، به تدریج و گام به گام نویز را از آن حذف می‌کنند تا یک تصویر واقعی و باکیفیت ایجاد کنند.

این فرآیند شبیه به انتشار در ترمودینامیک است، جایی که یک ماده (مثل جوهر) در یک مایع (مثل آب) پخش می‌شود تا یک ترکیب یکنواخت ایجاد کند. مدل‌های انتشار نیز به همین ترتیب، نویز را به تدریج از یک تصویر تصادفی خارج می‌کنند تا تصویر مورد نظر را به دست آورند.

مدل‌های انتشار به دلیل توانایی‌شان در تولید تصاویر بسیار واقعی و با جزئیات، به سرعت در حال تبدیل شدن به یکی از محبوب‌ترین ابزارها در حوزه تولید تصویر با هوش مصنوعی هستند. از تولید تصاویر هنری گرفته تا ویرایش و بهبود تصاویر موجود، مدل‌های انتشار پتانسیل بسیار زیادی دارند.

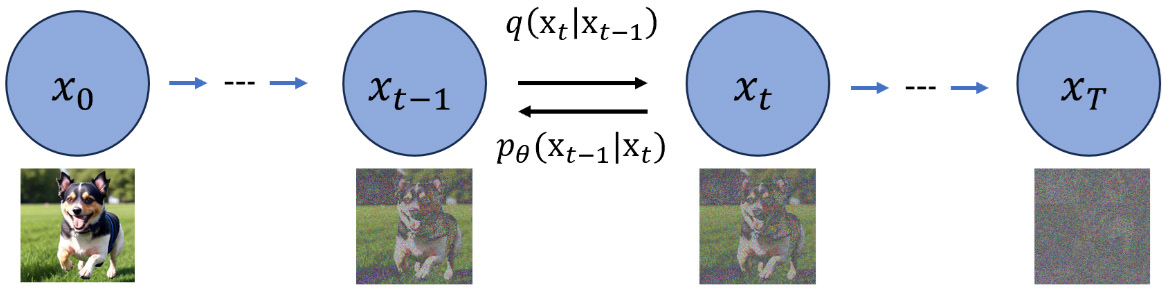
فرایند عکس به نویز

ما از فرآیند انتشار پیش‌تعیین‌شده به نام $\backslash (q\backslash )$ استفاده می‌کنیم که به طور سیستماتیک نویز گاوسی به یک تصویر اضافه می‌کند تا به نویز خالص برسد. این فرآیند با \(q(x_t|x_{t-1})\) نشان داده می‌شود. توجه داشته باشید که فرآیند معکوس \(p_{\theta}(x_{t-1}|x_t)\) هنوز مشخص نیست.

یک مرحله از فرآیند انتشار پیش‌رو به صورت زیر قابل بیان است:

\(q(x_t|x_{t-1}) := \mathcal{N}(x_t;\sqrt{1-\beta_{t}}x_{t-1},\beta_t I)\)

بیایید این فرمول را از چپ به راست توضیح دهیم:

• نماد \(q(x_t|x_{t-1})\) برای نشان دادن توزیع احتمال شرطی استفاده می‌شود. در این مورد، توزیع \(q\) احتمال مشاهده تصویر نویزی \(x_t\)​ را با توجه به تصویر قبلی \(x_{t-1}\)​ نشان می‌دهد.
• در فرمول از علامت := به جای علامت تیلدا (~) استفاده شده است، زیرا فرآیند انتشار پیش‌رو یک فرآیند قطعی است. علامت تیلدا (~) معمولاً برای نشان دادن یک توزیع استفاده می‌شود. در این مورد، اگر از علامت تیلدا استفاده می‌کردیم، فرمول بیان می‌کرد که تصویر نویزی یک توزیع گاوسی کامل است. با این حال، اینطور نیست. تصویر نویزی در مرحله \(t\) با یک تابع قطعی از تصویر قبلی و نویز اضافه شده تعریف می‌شود.
• \(\beta_t\) واریانس نویز در مرحله \(t\) است. \(\sqrt{1-\beta_{t}}x_{t-1}\) میانگین توزیع جدید است.

حال می‌خواهیم با استفاده از پایتون، به عکس بالا نویز گوسی اضافه کنیم:

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

# Load image
img_path = r"sherlok.jpg"
image = plt.imread(img_path) / 256

# Parameters
num_iterations = 16
beta = 0.1  # noise_variance
images = []

# Forward diffusion process
for i in range(num_iterations):
    mean = np.sqrt(1 - beta) * image
    image = np.random.normal(mean, beta, image.shape)
    # Convert to PIL image
    pil_image = Image.fromarray((image * 255).astype('uint8'), 'RGB')
    images.append(pil_image)

# Display images using matplotlib
fig, axes = plt.subplots(4, 4, figsize=(12, 12))
axes = axes.ravel()

for i, img in enumerate(images):
    axes[i].imshow(img)
    axes[i].set_title(f"Step: {i}", fontsize=10)
    axes[i].axis('off')

plt.tight_layout()
plt.show()

خروجی این کد، به صورت زیر می‌شود:

از نتیجه می‌توان دید که اگرچه هر تصویر از یک تابع توزیع نرمال (گاوسی) به دست آمده است، اما هر تصویر لزوماً توزیع گاوسی کامل نیست، یا دقیق‌تر بگوییم، توزیع گاوسی ایزوتروپیک (همه‌جهتی). تصویر تنها زمانی تبدیل به توزیع گاوسی کامل می‌شود که عدد گام به بی‌نهایت برسد. اما این لازم نیست. در مقاله اصلی DDPM، تعداد گام‌ها روی ۱۰۰۰ تنظیم شده است و بعداً در Stable Diffusion، این عدد به بین ۲۰ تا ۵۰ کاهش یافته است.

اگر تصویر آخر شکل بالا، یک توزیع گاوسی ایزوتروپیک باشد، نمایش دو بعدی آن به صورت یک دایره ظاهر می‌شود؛ زیرا این توزیع با داشتن واریانس‌های برابر در تمام ابعاد مشخص می‌شود. به عبارت دیگر، پخش یا عرض توزیع در تمام محورها یکسان است.

بیایید توزیع پیکسل‌های تصویر را پس از اضافه کردن نویز گاوسی در 16 مرحله رسم کنیم:

sample_img = image # take the last image from the diffusion process
plt.scatter(sample_img[:, 0], sample_img[:, 1], alpha=0.5)
plt.title("2D Isotropic Gaussian Distribution")
plt.xlabel("X")
plt.ylabel("Y")
plt.axis("equal")
plt.show()

خروجی این کد به صورت زیر است:

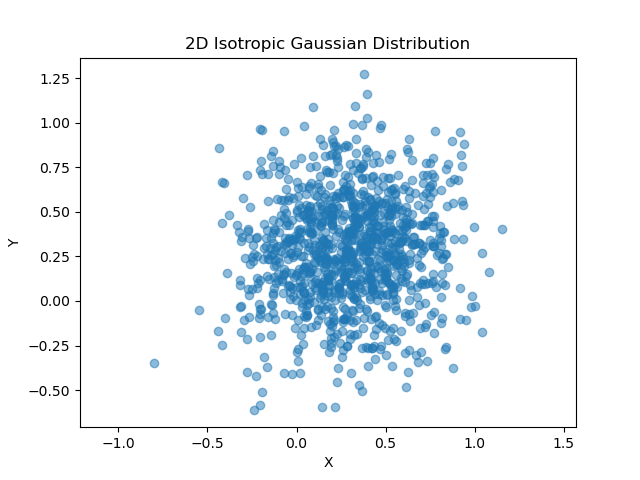
شکل نشان می‌دهد که کد چگونه به طور کارآمد یک تصویر را در تنها ۱۶ مرحله به یک تصویر نویز تقریباً همه‌جهت و نرمال تبدیل می‌کند، همانطور که در تصویر آخر نشان داده شده است.